Introducing Maxima

17 August 2009 Leave a comment Go to comments

Maxima is a computer algebra system. In other words, it is a mathematics software that is capable of symbolic manipulation. It is available for Windows as a command line interface



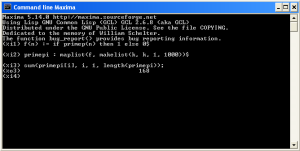
or as a graphical interface via wxMaxima:



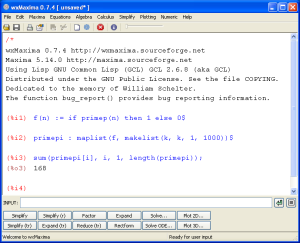
You can also use Maxima under Linux:



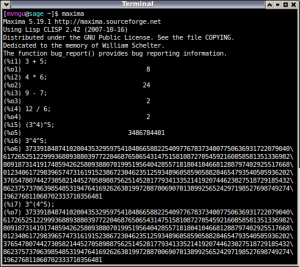
For a short introduction to Maxima, see this 10-minute tutorial. The Maxima website contains many types of documentation for learning Maxima, ranging from short tutorials to the Maxima manual.

Numbers and Arithmetics

Think of Maxima as a powerful calculator. To add two numbers, you use the addition operator “+”. You subtract two numbers using the subtraction operator “-“, multiply two numbers using “*”, and divide two numbers using “/”. Here are some examples of these in action:

(%i1) 3 + 5;
(%o1)                                  8
(%i2) 4 * 6;
(%o2)                                 24
(%i3) 9 - 7;
(%o3)                                  2
(%i4) 12 / 6;
(%o4)                                  2

For now, don’t worry too much about things like “(%i1)” and “(%o1)”. But you should know that “(%i1)” means input number 1, while “(%o1)” means output number 1. Exponentiation can be done using “^”. The order in which exponentiation is performed is important. You can control the order of operation using parentheses:

(%i8) 2^3;
(%o8)                                  8
(%i9) (2^3)^2;
(%o9)                                 64
(%i10) 2^(3^2);
(%o10)                                512
(%i11) 2^3^2;
(%o11)                                512

Use the exclamation mark “!” to do factorials:

(%i12) 2!;
(%o12)                                 2
(%i13) 3!;
(%o13)                                 6
(%i14) 4!;
(%o14)                                24

Lists

An easy way to create lists is via the opening square bracket “[” and the closing square bracket “]”. Here is a list of numbers:

(%i16) L : [2, 4, 6, 8];
(%o16)                           [2, 4, 6, 8]

The operator “:” is used for assigning something to a variable. In the above, we assign the list [1, 2, 3, 4] to the variable L. A list can have a
mixture of numbers and strings:

(%i17) L2 : [1, 2, 3, "a", "b", "c"];
(%o17)                        [1, 2, 3, a, b, c]

Unlike some programming languages (e.g. C, C++, Java, Python), lists defined in Maxima have their indices starting from 1. For the list L above, the first element 2 has index 1, the second element 4 has index 2, the third element 6 has index 3, and so on. The elements of a list are accessed using square brackets:

(%i22) L[1];
(%o22)                                 2
(%i23) L[2];
(%o23)                                 4
(%i24) L[3];
(%o24)                                 6
(%i25) L[4];
(%o25)                                 8

Use the command length() to find out the number of elements in a list. This command can also be used to loop through all elements of a list:

(%i29) length(L);
(%o29)                                 4
(%i30) for i:1 thru length(L) do print(L[i])$
2
4
6
8

Notice that the dollar sign “$” was used to suppress any output other than those of the command print(). Sometimes the dollar sign is used to suppress output because you might not be interested in viewing the output or the output is too long. Try these:

(%i31) 3^(4^5);
(%o31) 37339184874102004353295975418486658822540977678373400775063693172207904\
061726525122999368893880397722046876506543147515810872705459216085858135133698\
280918731419174859426258093880701995195640428557181804104668128879740292551766\
801234061729839657473161915238672304623512593489605859058828465479354050593620\
237654780744273058214452705898875625145281779341335214192074462302751872918543\
286237573706398548531947641692626381997288700690701389925652429719852769874927\
4196276811060702333710356481
(%i32) 3^(4^5)$

Lists can also be created using the command makelist(). A general syntax of this command is makelist(expr, i, i_0, i_n) where expr is an expression involving the variable i, with i starting from i_0 and ends at i_n. For example, here is how you can create a list of integers from 0 to 10:

(%i34) makelist(i, i, 0, 10);
(%o34)                [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

In this case our expression is just i, with the variable i going from 0 to 10. Here is a list of positive integer squares less than 30:

(%i36) makelist(i^2, i, 1, 5);
(%o36)                         [1, 4, 9, 16, 25]

and a list of reciprocals:

(%i37) makelist(1 / (i+2), i, 1, 10);
                        1  1  1  1  1  1  1  1   1   1
(%o37)                 [-, -, -, -, -, -, -, --, --, --]
                        3  4  5  6  7  8  9  10  11  12

In the last example, the expression is 1 / (i+2), the variable is i, which goes from 1 to 10.

The command sum() can add up all numbers in a range of values. You can sum all numbers within a range as follows:

(%i41) sum(i, i, 0, 10);
(%o41)                                55
(%i42) sum(i^3, i, 1, 5);
(%o42)                                225
(%i43) sum(1 / (i+2), i, 1, 10);
                                     44441
(%o43)                               -----
                                     27720

The command sum(i, i, 0, 10) implements the expression

\displaystyle{\sum_{i=0}^{10} i}

The command sum(i^3, i, 1, 5) implements the expression

\displaystyle{\sum_{i=1}^{5} i^3}

And the command sum(1 / (i+2), i, 1, 10) implements the expression

\displaystyle{\sum_{i=1}^{10} \frac{1}{i+2}}

The command sum() can also work with lists. The last three summations can also be done as follows:

(%i44) L : makelist(i, i, 0, 10);
(%o44)                [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
(%i45) L2 : makelist(i^3, i, 1, 5);
(%o45)                        [1, 8, 27, 64, 125]
(%i46) L3 : makelist(1 / (i+2), i, 1, 10);
                        1  1  1  1  1  1  1  1   1   1
(%o46)                 [-, -, -, -, -, -, -, --, --, --]
                        3  4  5  6  7  8  9  10  11  12
(%i47) sum(L[i], i, 1, length(L));
(%o47)                                55
(%i48) sum(L2[i], i, 1, length(L2));
(%o48)                                225
(%i49) sum(L3[i], i, 1, length(L3));
                                     44441
(%o49)                               -----
                                     27720

The command prod() can be used to multiply a range of numbers together. For instance, the expression

\displaystyle{\prod_{i=1}^{10} i}

can be computed in Maxima as

(%i58) prod(i, i, 1, 10);
(%o58)                              3628800

The expression

\displaystyle{\prod_{i=1}^{5} i^3}

can be evaluated as

(%i59) prod(i^3, i, 1, 5);
(%o59)                              1728000

And the expression

\displaystyle{\prod_{i=1}^{10} \frac{1}{i+2}}

is computed as

(%i60) prod(1 / (i+2), i, 1, 10);
                                       1
(%o60)                             ---------
                                   239500800

All of these three expressions can also be computed as follows:

(%i61) L : makelist(i, i, 1, 10);
(%o61)                  [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
(%i62) L2 : makelist(i^3, i, 1, 5);
(%o62)                        [1, 8, 27, 64, 125]
(%i63) L3 : makelist(1 / (i+2), i, 1, 10);
                        1  1  1  1  1  1  1  1   1   1
(%o63)                 [-, -, -, -, -, -, -, --, --, --]
                        3  4  5  6  7  8  9  10  11  12
(%i64) prod(L[i], i, 1, length(L));
(%o64)                              3628800
(%i65) prod(L2[i], i, 1, length(L2));
(%o65)                              1728000
(%i66) prod(L3[i], i, 1, length(L3));
                                       1
(%o66)                             ---------
                                   239500800

Functions and Maps

Maxima uses the “colon-equals” operator “:=” in order to create functions. Here is a function that returns 1 if the input is a prime number, and returns 0 otherwise. We then evaluate the function for some integer values.

(%i67) func(x) := if primep(x) then 1 else 0$
(%i70) func(1);
(%o70)                                 0
(%i71) func(2);
(%o71)                                 1
(%i72) func(3);
(%o72)                                 1
(%i73) func(4);
(%o73)                                 0
(%i74) func(5);
(%o74)                                 1
(%i75) func(6);
(%o75)                                 0
(%i76) func(7);
(%o76)                                 1
(%i77) func(8);
(%o77)                                 0
(%i78) func(9);
(%o78)                                 0

You can achieve the same effect by using the command maplist():

(%i80) maplist(func, makelist(i, i, 1, 9));
(%o80)                    [0, 1, 1, 0, 1, 0, 1, 0, 0]

As you can see, maplist() applies a function to every element of a list and then returns the results as another list. But you don’t have to create the function func() first. You can also use the command lambda() to achieve the same effect:

(%i81) maplist(lambda([x], if primep(x) then 1 else 0), makelist(i, i, 1, 9));
(%o81)                    [0, 1, 1, 0, 1, 0, 1, 0, 0]

As a final example, suppose you have a list of numbers from 1 to 100. If any number in the list is prime, you change that number to 1. If the number is not prime, you change it to 0. At the end of this computation, you would end up with a list of the same length as the original list, but the elements of the new list are 1’s and 0’s. To find the number of primes between 1 and 100, you sum the new list. Here is how to do so:

(%i85) L : makelist(i, i, 1, 100);
(%o85) [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39,
40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58,
59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77,
78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96,
97, 98, 99, 100]
(%i86) for i:1 thru length(L) do (
           if primep(L[i]) then
               L[i] : 1
           else
               L[i] : 0
       )$
(%i87) L;
(%o87) [0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1,
0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0,
0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]
(%i88) sum(L[i], i, 1, length(L));
(%o88)                                25

This means that there are 25 prime numbers between 1 and 100.

Categories: documentation, mathematics, Maxima, programming, symbolic computation Tags: , , , , ,
  1. Roberto
    25 August 2009 at 4:21 pm

    Cut my teeth on Mathematica 4.1 and learned a very little of Maple at a University while taking some courses. Was trying to figure out how to sum a 2000 element list with WxMaxima and just as I figured it out for myself (using L[i]), I stumbled on your perfectly presented blog on JUST my question. I always try to learn how to “sum a sequence” with any computer algebra tool as one of the first skills. It is surprising how many students don’t know even how to create a sequence while carrying around expensive TI-89 calculators and the like. (Lists or sequences are comma separated lists with curly braces in the TI series as in “{1,2,3,a,b,c} STO L1” will store the list/sequence {1,2,3,a,b,c} to one of the 6 built in lists (access by 2nd L1 on the yellow row just above “1” on the TI-83P) for example.

  2. Henderson
    18 January 2010 at 3:21 pm

    Thanks for that post!
    I was wondering whether there is a “built-in” function for getting the index of a List/Array-element?
    L : [10,2,10,4]$
    index : get_index(L, 10)$
    index; -> 3
    Best regards and thanks again!

  3. mvngu
    18 January 2010 at 3:42 pm

    @Henderson

    > I was wondering whether there is a “built-in” function for
    > getting the index of a List/Array-element?

    I have no idea. You might want to email the Maxima mailing list. See

    http://maxima.sourceforge.net/maximalist.html

  1. No trackbacks yet.

Leave a comment